炼丹笔记·必读论文
作者：炼丹小生
推荐系统的核心挑战在于解决高维稀疏的user-item矩阵推荐问题，如何基于百万用户的兴趣数据为单个用户推荐最感兴趣的item是一个复杂的任务。这篇论文《GLocal-K: Global and Local Kernels for Recommender Systems》提出了一个新的框架——Global Local Kernel-based matrix completion（GLocal-K），旨在解决高维稀疏的user-item矩阵补全问题。
简介
GLocal-K框架分为两个主要阶段。首先，我们通过局部核化权重矩阵预训练一个自动编码器，该编码器利用2D RBF核将数据从原始空间转换到特征空间。随后，预训练的自动编码器通过基于卷积的全局核对评分矩阵进行微调。
GLocal-K
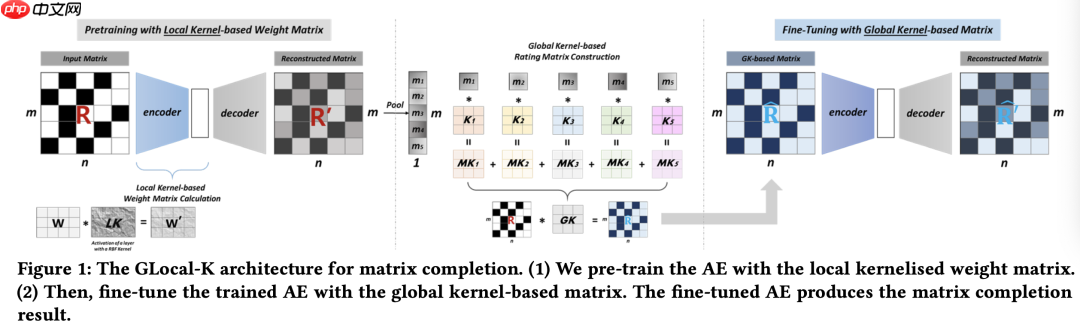
如下图所示，两个阶段分别使用了两种核：
预训练阶段 – 使用局部核化权重矩阵 微调阶段 – 使用基于全局核的矩阵 需要注意的是，在预训练阶段使用有限支持核使得密集连接更加密集，而稀疏连接更加稀疏。这篇论文关注的是矩阵补全，推断出矩阵R(m * n)中的所有评分，其中有n个用户和m个项目。i = {1, 2, …, m}，每个i由向量ri = (Ri1, Ri2, …, Rin)表示。
首先，训练一个基于项目的自动编码器，模型如下公式所示：
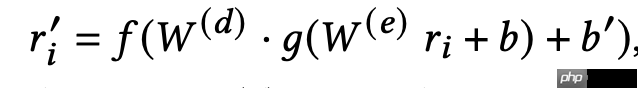W(e)是一个hm的矩阵，W(d)是一个mh的矩阵，b和b’是偏置项，f(.)和g(.)都是非线性激活函数。
为了强调密集和稀疏连接，论文重新参数化权重矩阵，在自动编码器中使用径向基函数（RBF）核，这是已知的核技巧。
RBF定义如下，K(.)就是RBF核函数，用于计算两个集合U/V向量之间的相似度。
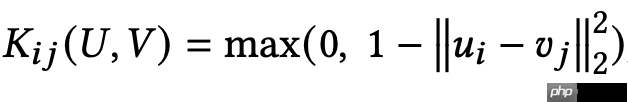核函数可以描述为一个核矩阵LK，如图所示，其中每个元素为1表示相同的向量，接近0表示ui和vj距离较远，然后我们就可以计算局部核化权重矩阵，如下所示：
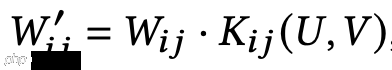W’是两个矩阵的Hadamard乘积得到的。向量U和V之间的距离决定了神经网络中神经元的连接，随着训练向量的变化，稀疏度也是动态变化的。将核技巧应用于权重矩阵可以正则化权重矩阵并学习到泛化更强的向量表示。
最后，使用评分矩阵对预训练的自动编码器进行微调。全局核的构建和应用过程如下：
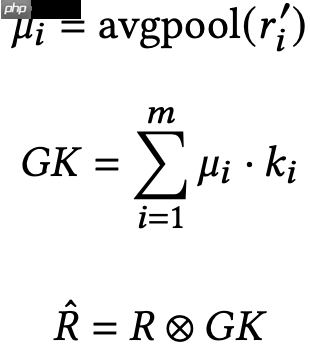如图所示，解码器已经输出了预训练模型，并且已经用预估的评分初始化了评分矩阵。通过基于项目的平均池化，总结了每个项目所有信息，得到池化结果M = {u1, u2, …, um}，然后使用多个核K = {k1, k2, …, km}（mt^2的矩阵），通过内积聚合池化结果，如图所示。聚合后的GK(t t)就是全局卷积核，并将其用于user-item矩阵的特征提取，作为微调的输入。
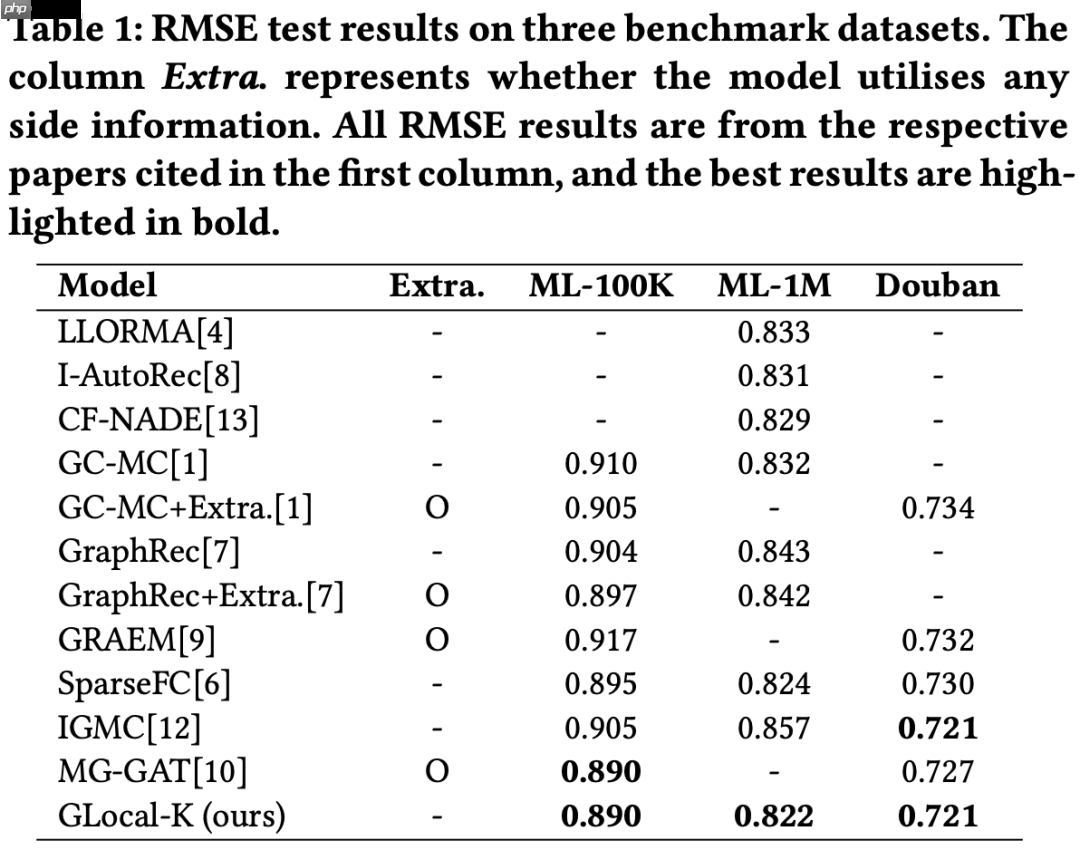
实验效果
参考文献
1、GLocal-K: Global and Local Kernels for Recommender Systems
